(This post is long! To avoid hiding the release announcement: bepuphysics 2.4 recently released! It's really fast!)

July 20, 2024 edit: Fixed a couple of errors in the post and added a note about saddle points. This is what I get for procrastinating three years before writing it up. Thanks to Erin Catto for working through it and noticing!

For bepuphysics2's collision detection, I needed a quick way to get a direction of (local) minimum depth for the more difficult convex collision pairs. Minkowski space methods based on support functions are common in collision detection, but the most popular algorithms don't quite cover what I wanted... So after a long journey, I found something (potentially) new. This is the journey to the tootbird.

If you're already familiar with GJK/MPR/EPA and just want to see descriptions of maybe-novel algorithms, you can skip a few sections ahead.

Background

Minkowski space collision detection methods are pretty handy. With nothing more than a function that returns the furthest point on a convex shape along a direction, you can do all sorts of useful things- boolean intersection testing, finding collision normals, separation distance, ray testing, and more.

Thanks to existing good explanations of the basic concepts, I'll skip them here.

The most common algorithms in this space are:

Gilbert-Johnson-Keerthi (GJK): Covered by the video above. Many variants exist; specialized boolean, ray, distance, and closest point queries are some of the more frequently seen uses. Often used to find closest points for 'shallow' collision detection with contact manifolds that are incrementally updated from frame to frame. Limited usefulness when shapes intersect; doesn't directly provide a local minimum depth.
Expanding Polytope Algorithm (EPA): Sometimes used for finding penetrating depths and collision normals. Conceptually simple: incrementally expand a polytope inside the minkowski difference by sampling the support functions until you reach the surface. It can be numerically tricky to implement and is often much slower than other options. When it is used, it is often as a fallback. For example, using GJK for shallow contact means that only deep intersections need to use EPA.
Minkowski Portal Refinement (MPR): From Gary Snethen, a different form of simplex evolution. For more information about how it works, see his website and the source, Pretty quick and relatively simple. As in GJK, variants exist. Boolean and ray queries are common, but it can also provide reasonably good estimates of penetration depth and normal for overlapping shapes. It doesn't guarantee convergence to depth local minima, but it often does well enough for game simulation- especially for simple polytopes that don't have any extreme dimensions.

~~EPA is pretty rare these days as far as I know~~ (incorrect!). The old bepuphysics1 used GJK for shallow contact with MPR as a deep fallback, optionally re-running MPR in the deep case to (sometimes) get closer to local minimum depth when the first result was likely to be noticeably wrong. It worked reasonably well, and caching the previous frame's state and results kept things pretty cheap.

Motivations in bepuphysics2

I had some specific goals in mind for bepuphysics2 collision detection:

One shot manifolds. Bepuphysics1 incrementally updated contact manifolds, with most pairs adding one contact per frame. There are ways to generate full manifolds with GJK/MPR and friends without resorting to feature clipping, but they typically involve some type of sampled approximation. I wanted the same level of quality and consistency that box-box face clipping offered whenever possible. Realistically, for most pairs, this meant manually clipping features against each other.
Deeply speculative contact constraints. The algorithm needs to be able to find an axis of (at least locally) minimum penetration depth at any depth or separation. Contact features could then be found from the minimum depth axis.
Vectorization. Multiple lanes of pairs are tested at once, scaling up to the machine execution width. This speeds up simple cases enormously, but makes complex state machines or jumping between algorithms like bepuphysics1 did impractical. I needed something that would work across the penetrating and separating cases cleanly.
Minimize weird tuning knobs, wonky behaviors, and content requirements. Any method used should be numerically stable and provide local minimum depths such that a user never sees shapes getting pushed out of each other along an obviously suboptimal direction.

Taken together, these goals aren't a good fit for the common Minkowski space approaches. For all collision pairs where it was feasible, I made special cases. Cylinders finally crossed the complexity event horizon, so I began looking for alternatives.

Gradient Methods

In the era of backprop, differentiable systems spew from every academic orifice. I figured I might as well give it a try even if I didn't expect much. It technically worked.

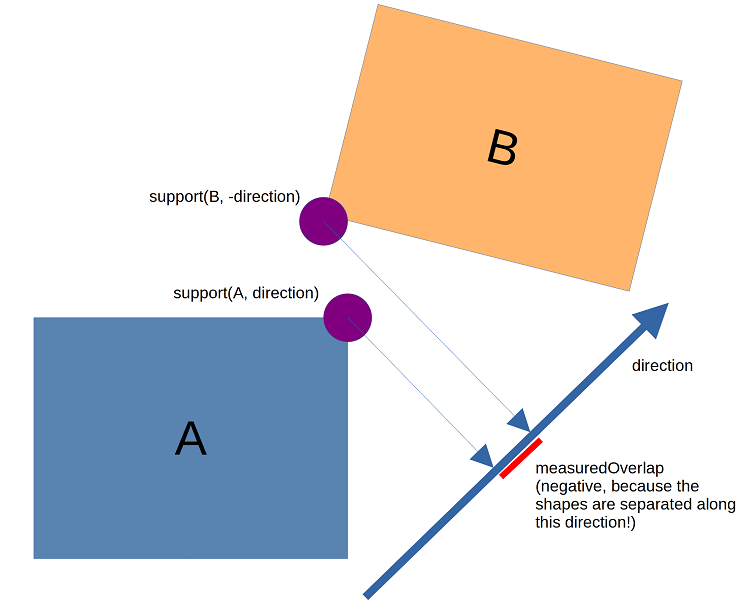
Conceptually, for two convex shapes, there exists a function expressing the depth measured along a given axis: measuredOverlap = dot(direction, support(shapeA, direction) - support(shapeB, -direction)) where support is a functioning returning the extreme point on the given shape in the given direction. The right side of the dot product is the Minkowski difference sample for the direction, but you can also intuitively think of it as just measuring the interval of overlap:

In a gradient based method, we want to repeatedly nudge the direction such that the depth gets lower. For some shapes, mainly those with nice smooth continuous surfaces, you can compute an analytic gradient that is reasonably informative. In those cases, convergence can be quick. But convex hulls and other shapes with surface discontinuities make convergence more difficult. The depth landscape tends to have a lot of valleys that make the search bounce from wall to wall rather than toward the goal, and getting an informative gradient can require numerically constructing it from multiple samples.

Nelder-Mead, an older numerical approach that doesn't require explicit derivatives, ended up being one of the more reliable options I tried.

I did not try any of the newer gradient methods (Adam and beyond); there's room to do better than my early experiments. They would help avoid some of the worst oscillation patterns that naïve gradient descent exhibits in valleys. Unfortunately, even with that, I suspect the iteration counts required for the target precision would become prohibitive. The above video uses 51 support samples to converge. Stopping early tends to yield noticeably bad behavior.

Poking Planes

Desiring alternative direction update rules, I scribbled on paper for several hours.

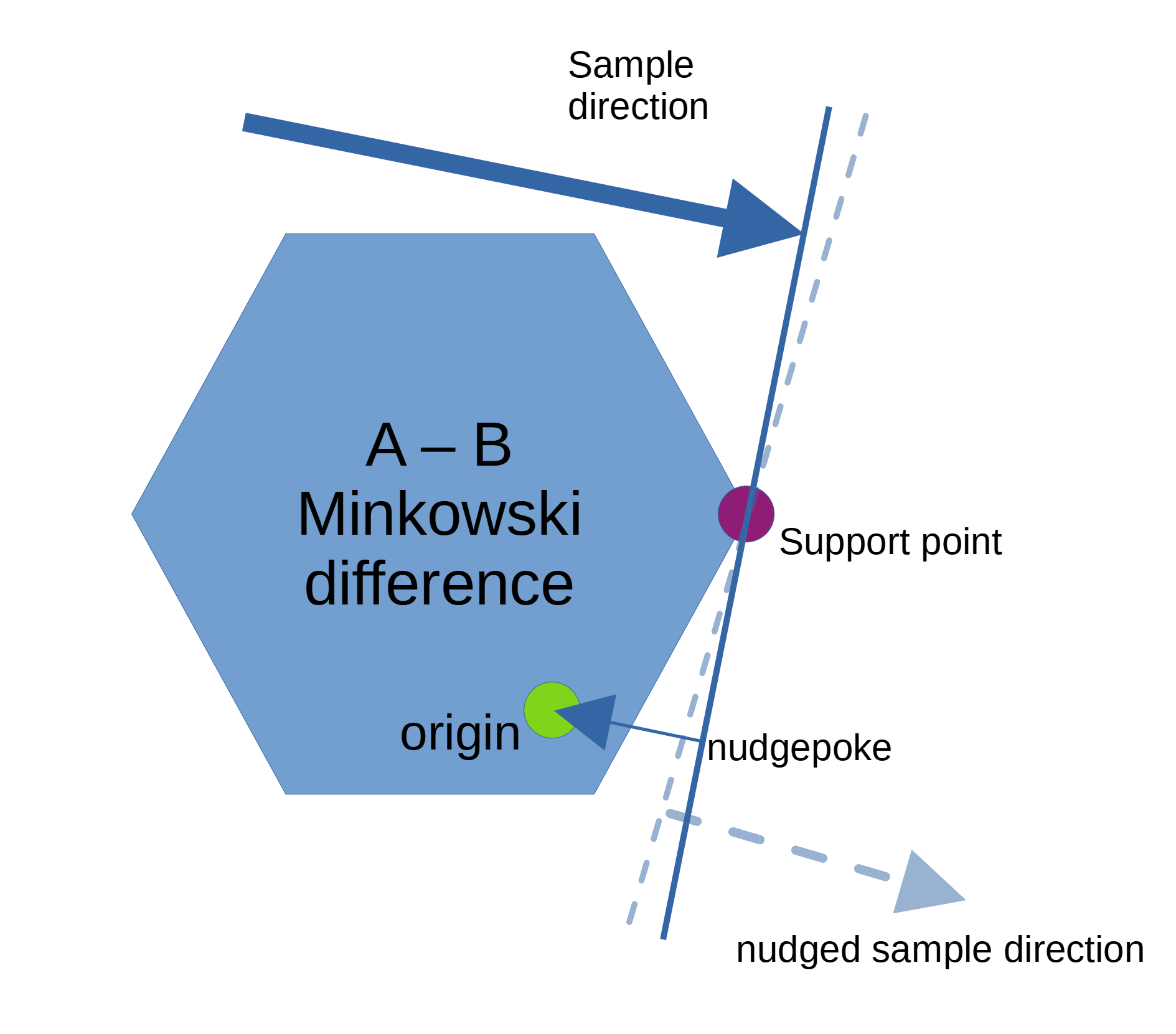
The support function for the Minkowski difference forms a support plane. If you think of the support point as a fulcrum and push the plane toward the Minkowski space origin in the overlapping case (the origin is contained in the Minkowski difference), you make progress towards a local minimum depth.

A simple update rule: incrementally tilt the support plane towards the minkowski origin. But how hard do you poke the plane? Too hard, and the plane will tilt past the local minimum and you can end up oscillating or fully diverging. Too gentle, and convergence will take forever.

I fiddled with this a bit. Any time depth increased, it was considered an overshoot and the search would take a half step back, repeating until it got to a point that was better than the pre-overshoot sample. Further, it would reduce the future step size attempt under the assumption that the goal was near. The step size was allowed to grow a little if no overshoot was observed.

It worked reasonably well, but there's a bit of a discontinuity when the support plane goes past the origin. At first, I just did some janky special casing, but it was a bit gross.

The Tootbird Dances Furtively

After some further scribbling, I realized I had been a bit of a doof.

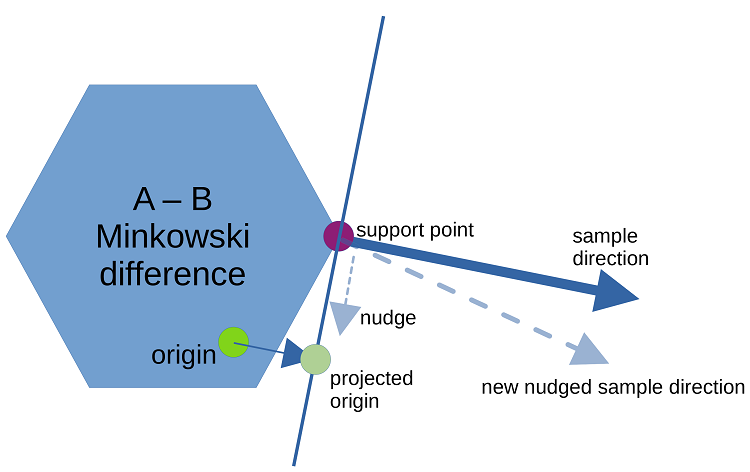
There was no need to conditionally 'push' or 'pull' the plane based on the origin's position relative to the support plane. The sample direction simply needed to move toward the origin projected onto the support plane.

The implementation, dubbed PlaneWalker, used multiple termination conditions: sufficiently small incremental changes to the best observed plane did not find depth improvements, the support point is perfectly lined up with the origin + supportDirection * depth, the discovered depth is lower than the minimum depth (that is, sufficiently negative that the implied separation is larger than the speculative margin), or the maximum iteration count has been reached.

This basic approach actually worked surprisingly well for smooth surfaces, where it tended to significantly outperform GJK and MPR by having a similar iteration count but much simpler individual iterations. This yielded a degree of stokedness.

I experimented with different kinds of history tracking- for example, using the closest point to the origin on the line segment connecting the current overshooting support to the previous support as a guess for the next direction. It helped a bit.

Unfortunately, when the minimal depth direction is associated with a flat surface, plane tilting tends to oscillate back and forth over the surface normal. It still converges by taking progressively smaller steps, but most shapes have flat surfaces, and flat surfaces are very frequently the support feature of minimum depth. GJK and MPR, in contrast, tend to handle polytopes extremely easily. They can sometimes converge to an answer in just a few iterations even without warm starting.

(Even though I didn't end up using the PlaneWalker for any of the current collision pairs, it still works well enough that I suspect I'll find uses for something like it later. It also happens to generalize to higher dimensions trivially...)

The Tootbird Rises

Further scribbling. I tried out a SimplexWalker that extended the PlaneWalker history tracking, which sometimes kinda-sorta helped, but not proportional to the added complexity. I experimented with something that ended up looking like MPR's portal discovery phase (if you squinted) using the projected origin as a dynamic goal, which worked, but the simplex update I was using didn't work in the separating case.

So I began fiddling again with another simplex update rule. Something a bit more GJK-ish- taking the closest point on the existing simplex to a search target... but what search target? Chasing the origin projected on the current support plane is unstable without strong constraints on what support planes are picked- the search target must provably avoid cycles, or else the simplex will never catch it. Using the origin as a search target avoids this issue; that's what GJK does. But finding the origin within the Minkowski difference tells you little about how separate those shapes. So... what search target is immune to cycles, and when sought, finds a local minimum...?

And here, the complete and True Tootbird cast aside the veil and revealed itself: the Minkowski space origin projected ~~onto~~ up to the least-depth-so-far-observed support plane.

July 20, 2024 edit: Corrected subtlety I had forgotten about when writing this up. Pulling the origin down to the support plane in the separating case is unnecessary and can hurt convergence in the separating case.

The tootbird could potentially move every iteration. If a support sample found a lesser depth, the tootbird would jump to the new location. Since the tootbird only updates to a lesser depth, chasing it will never cause you to run in circles indefinitely.

Thus, a Tootbird Search is a member of the family of algorithms which incrementally seek the tootbird. Note that the earlier PlaneWalker is technically not a tootbird search, since its objective was always the origin projected on the current support plane even though it did cache the best support plane for backtracking. (It would be pretty simple to make a PlaneWalker variant that was a tootbird search...)

A sample progression of tootbirds with a questionable update rule.

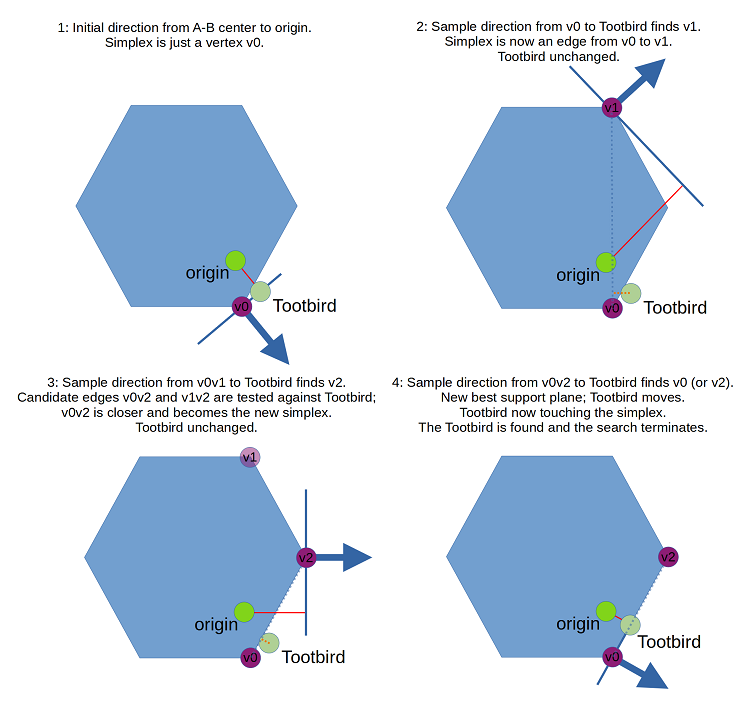
The bepuphysics2 DepthRefiner puts this together with a GJK-style simplex update, yielding a very potent optimizer. A version of the DepthRefiner implementing a 2D tootbird search would look like this:

Notice that the simplex in the 2D case never contains more than 2 vertices at one time. The tootbird, by virtue of being on the best-observed support plane, is always outside the Minkowski difference. At most, the simplex can touch the tootbird, but the tootbird cannot be contained. There's no need for the simplex to cover an area (or a volume, in 3D). Further, while we do want to choose the closest simplex when a new sample offers a choice, there is no need to explicitly calculate distances for all candidate simplices. For example, in the 2D case:

The only significant thing that changes when moving to 3D is that the simplex can become a triangle, and a step can require figuring out which of three potential triangles is the best choice. As in 2D, there's no need to calculate the actual distance for every candidate.

Create edges between the existing vertices A, B, and C and the step's new sample point D. Create a plane for each edge and check which side of the plane the tootbird is on. Based on the signs of the plane tests, you can know which subtriangle (BCD, CAD, or ABD) should be used as the next simplex. This is most clearly visible when D's projection along ABC's normal onto ABC is within ABC:

When D is outside ABC, things are a bit muddier and it's possible for the tootbird to not fall cleanly into any subtriangle by plane tests. This is a pretty rare circumstance, and my implementation shrugs and just takes ABD arbitrarily. This won't cause cycles; the tootbird only changes when a depth improvement is found, so even if our next simplex is a poor choice, it will have a path to march towards the tootbird and possibly improve upon it. You could do something more clever if you'd like.

Once a subtriangle is chosen, the closest offset from triangle to tootbird gives us our next search direction, similar to GJK except with the tootbird as the target rather than the origin.

(My implementation currently has one case where it doesn't use the raw offset as a search direction: when the tootbird is very close to but outside the simplex, the search direction can end up pointing about 90 degrees off of a previous search direction. In some cases, I found this to slow down convergence a bit, so I included a fallback that instead nudges the search direction toward the offset direction rather than taking the offset direction directly. This is similar in concept to the plane tilting described earlier. I'm on the fence on whether this is actually worth doing; the measured impact is pretty minimal, and there are cases where doing the fallback can slow down convergence.)

Drawing full execution diagrams for the 3D version is harder, but there is technically a debug visualizer in the demos. It visualizes the Minkowski difference explicitly through sampling and shows the progress of the simplex for each step. Unfortunately, the interior of flat surfaces on the Minkowski difference are never sampled, so the visualization requires some getting used to. But it's there if you want to play with it!

1. In DepthRefiner.tt, set the debug flag to true in the template code,
2. Uncomment the DepthRefinerTestDemo.cs,
3. Add DepthRefinerTestDemo to the DemoSet options,
4. Then try to visually parse this. Or not.

The DepthRefiner implementation terminates when the tootbird is touched by the simplex. A maximum iteration count in the outer loop also helps avoid numerical corner cases.

Notably, once a separating axis is identified (any support direction with a negative measured overlap), a tootbird search could fall back to seeking the origin. The DepthRefiner implementation keeps things simple and sticks to the tootbird at the moment, but depending on the implementation and pair being tested, having a special case for this might be worth it. It would require modifying the termination condition as well.

July 20, 2024 edit: Oops! I forgot; the tootbird is only projected up to the so-far best support plane. It is not pulled down in the separating case; this is just a clamp and accomplishes basically the same thing as using the origin in the separating case without execution divergence.

Further, there's nothing about tootbird search that requires a GJK-ish simplex update. It's just simple and fast. If you squint your eyes a bit, there's also a similarity between the described simplex update and MPR's portal refinement. I'd bet there are some other simplex updates floating out there that would work well with the guarantees provided by the tootbird, too!

Algorithm Extensions

The DepthRefiner tootbird search shares many properties of other Minkowski space collision detection methods. For example, in bepuphysics2, some collision pairs use an implementation which tracks the per-shape contributions to the Minkowski space support point (sometimes termed 'witnesses'). When the algorithm terminates, these witness points along with their barycentric weights corresponding to the closest point on the simplex at termination allow the closest point on shape A to be reconstructed. This is commonly done in other methods like MPR and GJK.

Warm starting is also an important piece of many Minkowski space methods. With a good guess at the initial simplex or search direction, the number of iterations required can drop significantly. Bepuphysics2's implementation of tootbird search does not currently do this, though it is on the to do list and the algorithm itself is compatible with warm starting.

Be careful with warm starting; the algorithm is not guaranteed to converge to a global minimum in all cases. Starting the search process with a bad guess (for example, the direction pointing from the origin to the Minkowski difference's center, rather than from the center to the origin) can easily result in the search converging to a bad local minimum.

Notes on Vectorization

The implementation within bepuphysics2 processes multiple collision pairs simultaneously across SIMD lanes. As a result, performance considerations are similar to GPU shaders: execution divergence and data divergence are the enemy.

To avoid too many conditional paths, the implementation tries to simplify and unify control flow. For example, thanks to the relatively low cost of the worst case simplex update, every single iteration executes the same set of instructions that assume the worst case triangular simplex. When the simplex is actually a point or edge, the empty slots are filled out with copies, yielding a degenerate triangle.

The implementation still contains conditions, but not as many as a fully sequential implementation could take advantage of. The main loop will continue to run until every lane completes. Given that execution batches share the same involved shape types, the number of required iterations is often similar, but this is another area where a sequential implementation would be able to extract more some value. Overall, the widely vectorized version with 256 bit vectors still usually has an advantage, but a sequential narrow vectorization (that is, trying to accelerate only one collision pair as much as possible, rather than doing N pairs quickly) should still be very quick.

For shapes with implicit support functions, like cylinders, support function vectorization is trivial. Data driven types like convex hulls require more work. A vector bundle of shapes could contain hulls with different numbers of vertices, so vectorizing over shapes would require an expensive gather/transpose step and have to always run worst-case-across-bundle enumerations. Convex hulls instead preprocess their internal representation into an AOSOA format and bundle support functions evaluate each shape independently. The support function outputs are transposed back into vector bundles for use by the outer loop.

For readers unfamiliar with modern C# wondering how SIMD is used, in the DepthRefiner it's predominantly through the Vector<T> API. Vector<T> holds a SIMD vector of runtime/architecture defined length. On an old machine limited to SSE42, it could hold 4 single precision floats. On an AVX2 machine, it'll be 8 single precision floats. When the DepthRefiner was written, this (along with types like Vector4) was the main way to take advantage of SIMD in C#. The (compile time) variable width and cross platform requirement meant that many operations were not directly exposed. Shuffles, for example, were a challenge.

In the short time since then, access to vectorization has improved significantly. Hardware specific intrinsics give you the lowest level operations available. More recently (.NET 7 previews), convenience APIs on the fixed-width Vector256<T> and friends are providing the best of both worlds- readable code with high performance that works across multiple architectures. Bepuphysics2 has already adopted the lower level intrinsics in a few hot paths, and there are areas in the DepthRefiner where they'd be useful but are not yet included.

In other words, the DepthRefiner is already a bit old at this point. Some of the implementation choices were dictated by a lack of time, or what options were available. Don't assume that the implementation as-is is the fastest it can possibly be, and feel free to experiment.

Convergence

Given a static tootbird (and leaving aside the current implementation's more complex fallback search direction nudge), the simplex update has the same convergence behavior as GJK when the origin is outside the minkowski difference.

During execution, the tootbird can move, but only if an improvement to depth has been found. It cannot cycle back to higher depth. Since depth is monotonically decreasing over execution, the tootbird will eventually settle into a local or global minimum. At that point, it can be treated as static, and the convergence properties of GJK apply.

In practice, the simplex and tootbird move rapidly together and settle on a local minimum quickly. The number of iterations required is similar to GJK in my experiments. The per-step cost is lower, given the guarantees provided by the tootbird being outside of the Minkowski difference. I would expect the performance to be similar and depend on details of implementation and use case.

July 20, 2024 edit: In addition to potentially converging to a local minimum when initialized with a misleading initial search direction, the depth refiner can also get caught on a saddle point if initialized such that the tootbird is on the support plane. This could be mitigated, but the implementation in bepuphysics2 makes no attempt to do so because saddle points are both pretty rare and unstable in dynamic simulation. This may be worth handling in other contexts.

So, empirically, does it work, and is it fast enough?

Yup!

FAQ

Q: okay but why is it called tootbird

A: what do you mean